问任何一个物理爱好者,什么是量子力学?他们很可能会提到“薛定谔的猫”。接下来呢?则可能是薛定谔方程。但是这个方程究竟是什么,为什么它如此重要,以至于任何一个量子物理学家都会把它记在脑海中?1 月 7 日,在第十八期《张朝阳的物理课》上,搜狐创始人、董事局主席兼 CEO 张朝阳在直播间再现薛定谔方程奇妙的发现过程,初步揭秘量子力学的核心理论。
在直播间里,张朝阳带领大家简单复习前两节课的要点,并重点回顾经典力学中描述粒子和波的方式。在经典物理中,力的作用导致粒子运动状态的改变,可以用牛顿第二定律来描述这个改变过程。粒子的运动状态由位置和速度来表征,力的作用会改变粒子的速度,从而改变其能量。而在量子力学中,粒子由波函数来描述。在此,张朝阳先向网友介绍了经典力学中对波的描述方式。以一维波为例,在经典力学中,波由相应的波动方程来描述:
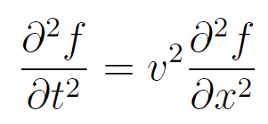
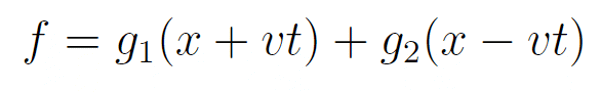
它示向左传播和向右传播的波的叠加。以平面波为例,描述平面波的 2 个主要参数为圆频率 ω=2πf 和波数 k=2π/λ。其中 λ 为波长,f 为频率。
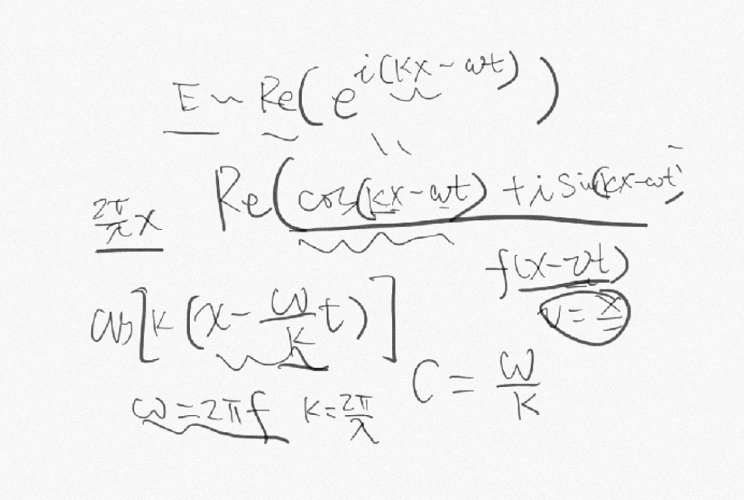
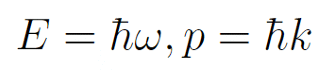
“我们努力地猜,当年薛定谔是怎么想到这个方程的?他看到德布罗意的论文之后,意识到电子应该用波来描述,于是把电磁波的想法转移过来,猜出了这个方程,最后居然是对的。”张朝阳像说故事一样引出今天的主题。
德布罗意提出物质波的时候只是给出了波长和动量的关系,但是并没有推导物质波如何演化。那么,薛定谔是如何猜出这个方程的呢?直播过程中,张朝阳做了详细生动的介绍。
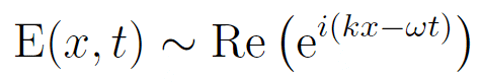
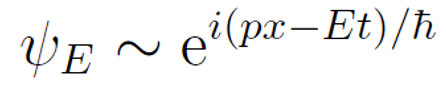
这就是薛定谔猜测的物质波的平面波形式。出于简洁的需求,张朝阳先考虑了一维自由粒子的情况。其能量和动量满足如下关系:
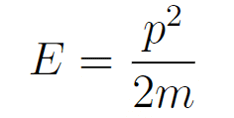
它在量子力学下是否依然满足呢?薛定谔对此作出了勇敢的假设,认为这个关系在非相对论量子力学框架内依然成立。那怎样在波函数上体现出这个关系呢?这就需要先将物质平面波中的动量和能量“取”出来。
至此,张朝阳开始介绍求导得出动量和能量的方法。在平面波的式子中,动量和能量都出现在指数上,但是只要我们对位置 x 和时间 t 求偏导数,相应的动量和能量不就下来了吗?于是,张朝阳又展示了如下推导:
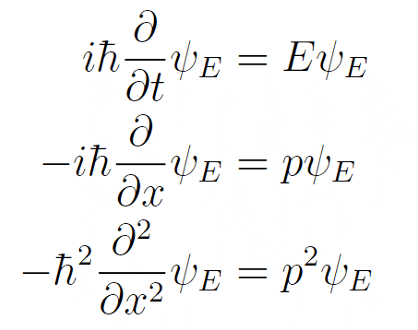
组合在一起就得到了有关这个平面波函数的方程。张朝阳强调,这个方程是线性偏微分方程,因此,它的各个解的线性组合,依然是原方程的解,这从形式上也符合量子力学的叠加原理。既然这个方程对平面波成立,而一般的波都可以看作是平面波的组合,那么这个方程对一般的自由物质波也成立。这就得到了一维自由粒子的波动方程:
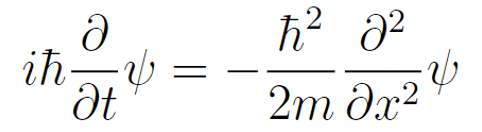
此时,张朝阳顺势介绍,当存在外部势场时,能量将不仅包含粒子动能,还应当包含势能:
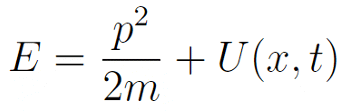
其中 U (x,t) 是势能函数。结合前面的推导,就得到了著名的一维薛定谔方程:
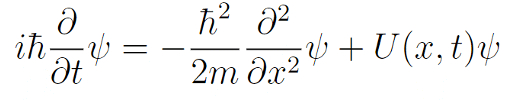

张朝阳介绍,薛定谔方程不是推导出来的,而是猜测出来的。它是非相对论量子力学的基本方程,具有公设性质。只有根据薛定谔方程计算出结果,与实验结果一致,我们才能说这个理论是对的。他还解释,薛定谔方程的左边是对时间的一次导数,而右边是对空间的二次导数,这一点很关键。且考虑到因子 i 的存在,波函数不像电磁场那样是实函数,而是复函数。
不过,即使薛定谔猜出了波动方程,也不知道这个波的物理意义是什么。张朝阳由此引入量子力学的哥本哈根诠释,也就是所谓的统计诠释。
张朝阳介绍,“波函数的模方,表示的是粒子出现在相应位置的概率密度,根据这个概率密度,我们只需要对特定区域积分,就可以得到在该区域上发现粒子的概率。当我们得到粒子的波函数时,我们并不知道粒子具体在哪,我们得到的信息仅仅是测量后粒子在各位置出现的概率。”他还进一步介绍波函数归一化的概念。具体地来说,因为整个空间上发现粒子的概率是 1,于是波函数的模方在整个空间上的积分就等于 1。
此外,张朝阳还提到矩阵力学和波动力学的关系,他说,“它们就像一座高山上的两条路径”。换言之,矩阵力学和波动力学都是描述量子力学的正确方法,是相互等价的。
张朝阳再次演示,在量子力学中,粒子的速度不再等于 ω/k,而应该等于相应的波的群速度 dω/dk。根据张朝阳的计算,ω/k 实际上等于 v / 2,为粒子速度的一半。如果使用群速度 dω/dk 来计算,则得到了正确的速度 v。他解释道,这是因为粒子在实际观测中以波包的形式存在,群速度是描述整个波包的移动速度的,因此正好对应于粒子的速度;而 ω/k 是等相位点的移动速度,不代表粒子的运动速度。

“我们今天理解了薛定谔是怎么猜到薛定谔方程的,也知道描述具有波粒二象性的微观粒子的波函数。后面,我们只要解这个方程,就能把天下所有事情给它算出来。”直播尾声,他回顾这一课的主要内容时说。同时他鼓励网友,量子力学很难懂,“会用很多堂课来讲。”据了解,下一讲他将开始解薛定谔方程,来解释氢的光谱,求一些波函数的定解,以及薛定谔方程的各种应用。
1. 凡本网注明“来源:消费日报网” 的所有作品,版权均属于消费日报网。如转载,须注明“来源:消费日报网”。违反上述声明者,本网将追究其相关法律责任。
2. 凡本网注明 “来源:XXX(非消费日报网)” 的作品,均转载自其它媒体,转载目的在于传递更多信息,并不代表本网赞同其观点和对其线. 任何单位或个人认为消费日报网的内容可能涉嫌侵犯其合法权益,应及时向消费日报网书面反馈,并提供相关证明材料和理由,本网站在收到上述文件并审核后,会采取相应措施。
4. 消费日报网对于任何包含、经由链接、下载或其它途径所获得的有关本网站的任何内容、信息或广告,不声明或保证其正确性或可靠性。用户自行承担使用本网站的风险。
5. 基于技术和不可预见的原因而导致的服务中断,或者因用户的非法操作而造成的损失,消费日报网不负责任。
